一、极限
1.数列极限
1.1 定义
定义: ,有
,有 。
。
1.2 几何解释

1.3 性质
唯一性:收敛数列的极限唯一,数列收敛则极限唯一;
有界性:收敛数列一定有界,数列收敛则必有界,有界但不一定收敛;
保号性:收敛数列具有保号性,当数列极限趋于a时,那就存在一个正整数N,使得n>N时,数列值与a保持同号。
同理性:收敛数列的任一子数列收敛于同一极限,若两个子数列收敛于不同的极限,则原数列必发散。
2.函数极限
2.1 自变量x趋于有限值时的函数极限
2.1.1  语言
语言
 , 当
, 当 时,恒有
时,恒有 。
。
2.1.2 几何解释
找一个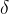 在
在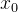 的一个
的一个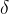 领域
领域 ,只要x落在
,只要x落在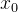 为中心,以
为中心,以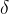 为距离的小区域里,使得函数值都落在这个领域内。
为距离的小区域里,使得函数值都落在这个领域内。

- 当
 时f
时f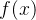 的极限存在
的极限存在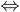 左右极限均存在且相等。如果
左右极限均存在且相等。如果 中有一个不存在,或者两个虽然存在,但是不相等,则
中有一个不存在,或者两个虽然存在,但是不相等,则 不存在.
不存在.
2.2 自变量x区域无穷大时的函数极限
2.1.1  语言
语言
 ,当
,当 时,恒有
时,恒有 .
.
2.1.2 几何解释

2.3函数极限的性质
唯一性:函数极限唯一
局部有界性:如果 ,那么存在常数
,那么存在常数 (界)和
(界)和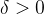 ,使
,使 (局部)时,有
(局部)时,有 .
.
局部保号性:如果 ,且A>0(或A<0),那么存在常数
,且A>0(或A<0),那么存在常数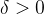 ,使得
,使得 (局部)时,有
(局部)时,有 (或
(或 ).
).
3.夹逼定理

4.基本求极限方法
4.1 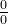 型
型
常用方法:洛必达法则
等价无穷小代换
泰勒公式
4.2  型
型
常用方法:洛必达法则
分子分母同除以分子和分母各项中最高阶的无穷大
基本极限,分子分母最高项
4.3  型
型
常用方法:同分化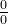 (适用于分式差)
(适用于分式差)
根式有理化(适用于根式差)
提无穷因子,然后等价代换或变量代换(t=1/x)、泰勒公式
4.4  型
型
常用方法:f(x)由分子变为分母 ,化为
,化为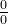 型或
型或  型。
型。
4.5  型
型
常用方法:凑基本极限![\lim_{}[1+\varphi (x)]^{\frac{1}{\varphi (x)}}=e](https://latex.csdn.net/eq?%5Clim_%7B%7D%5B1+%5Cvarphi%20%28x%29%5D%5E%7B%5Cfrac%7B1%7D%7B%5Cvarphi%20%28x%29%7D%7D%3De) ,其中
,其中 ;
;
改写成指数![\lim_{}[f(x)]^{g(x)}=\lim_{}e^{g(x)lnf(x)}](https://latex.csdn.net/eq?%5Clim_%7B%7D%5Bf%28x%29%5D%5E%7Bg%28x%29%7D%3D%5Clim_%7B%7De%5E%7Bg%28x%29lnf%28x%29%7D) ,使用洛必达法则;
,使用洛必达法则;
利用结论:若 且
且 则
则 ![\lim_{}[1+\alpha (x)^{\beta (x)}]=e^{A}](https://latex.csdn.net/eq?%5Clim_%7B%7D%5B1+%5Calpha%20%28x%29%5E%7B%5Cbeta%20%28x%29%7D%5D%3De%5E%7BA%7D)
4.5  和
和 型
型
此类函数一定是幂指函数,即 ,求解的方法是将其改写成指数形式
,求解的方法是将其改写成指数形式![\lim_{}[f(x)]g(x)=\lim_{}e^{g(x)*lnf(x)}](https://latex.csdn.net/eq?%5Clim_%7B%7D%5Bf%28x%29%5Dg%28x%29%3D%5Clim_%7B%7De%5E%7Bg%28x%29*lnf%28x%29%7D) ,从而化成
,从而化成 .
.
5.洛必达法则与等价无穷小
5.1洛必达法则
在一定条件下通过分子分母分别求导再求极限确定未定式值的方法。
5.2等价无穷小

二、导数
导数(Derivative),也叫导函数值。又名微商,是微积分中的重要基础概念。当函数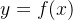 的自变量x在一点
的自变量x在一点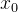 上产生一个增量
上产生一个增量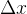 时,函数输出值的增量
时,函数输出值的增量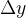 与自变量增量Δx的比值在
与自变量增量Δx的比值在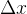 趋于0时的极限a如果存在,a即为在
趋于0时的极限a如果存在,a即为在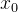 处的导数,记作
处的导数,记作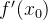 或
或 。
。
2.1导数的几何解释

2.2基本求导公式

三、偏导数
在数学中,一个多变量的函数的偏导数,就是它关于其中一个变量的导数而保持其他变量恒定(相对于全导数,在其中所有变量都允许变化)。
3.1 x方向的偏导
设有二元函数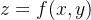 ,点
,点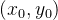 是其定义域D 内一点。把 y 固定在
是其定义域D 内一点。把 y 固定在 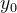 而让 x 在
而让 x 在 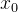 有增量
有增量 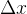 ,相应地函数
,相应地函数 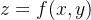 有增量,
有增量, 。
。
如果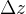 与
与 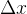 之比当 △x→0 时的极限存在,那么此极限值称为函数
之比当 △x→0 时的极限存在,那么此极限值称为函数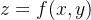 在
在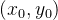 处对 x 的偏导数,记作
处对 x 的偏导数,记作 或函数
或函数 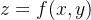 在
在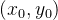 处对 x 的偏导数,实际上就是把 y 固定在
处对 x 的偏导数,实际上就是把 y 固定在 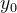 看成常数后,一元函数
看成常数后,一元函数 在
在 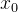 处的导数。
处的导数。
3.2 y方向的偏导
同样,把 x 固定在 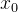 ,让 y 有增量
,让 y 有增量 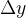 ,如果极限存在那么此极限称为函数
,如果极限存在那么此极限称为函数 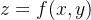 在
在 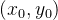 处对 y 的偏导数。记作
处对 y 的偏导数。记作 。
。
 4034
4034
 4034
4034
 434
434
 434
434



 获取中
获取中

 扫码支付
扫码支付
 点击重新获取
点击重新获取


 扫码支付
扫码支付
 余额充值
余额充值
wanderlus_ter: 拉普拉斯反变换公式是不是写错了
梦落残阳: 世界就需要你这样的人,nice
岗小李: 确实写错了,感谢!
sodcsdn: 欧拉公式写错了,是+1,写成-1了